In order to improve above approximation, we proposed another method
to calculate cascade decays of SUSY particles; connecting the production
amplitude of 
and
the decay amplitudes of 
and 
with taking into account helicity of each particle.
Since cutting points are at 
and 
whose width is very narrow,
then we can expect a good agreement with an exact method.
The method will be explained in a simple example;
assuming a particle 4 being an anti-fermion.
An exact expression of this cross section is
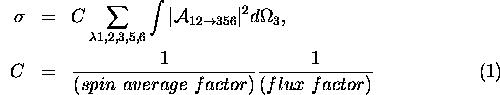
where 
is helicity state of i'th particle,
an amplitude of a 3-body process
and 
a 3-body phase space.
A 2-body scattering amplitude (
) and a 2-body decay
amplitude (
) can be written as;
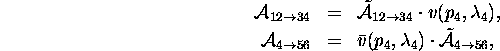
where v is a wave function of a particle 4.
A four-momentum of a particle 4, 
, is assumed to be on-shell
(
),
where 
is a mass of a particle 4.
By using these expression, a 3-body cross section can be expressed as;
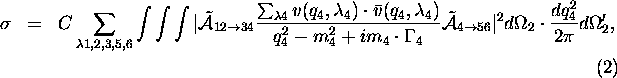
where 
is a four-momentum squared of an (internal) particle 4
(
), 
(
) a 2-body scattering
(decay) phase space, and 
the total width of particle 4.
If a narrow-width approximation is applied, a numerator of a propagator will be
replaced by on-shell wave functions and integration of a denominator
can be performed independently as;
Then,
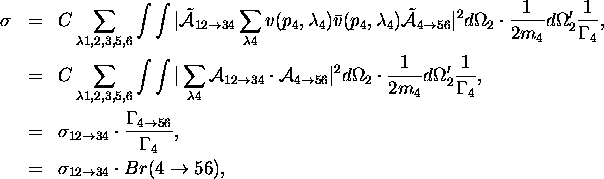
where 
(
)
is a partial width (a branching ratio) of a decay 
and
a total cross section of a 2-body process
. A factor 
works as a flux factor for a decay
phase-space integration.
In this method, the off-diagonal part of a spin summation
(for example
) is included as well as the diagonal ones.
These terms will disappear in total
cross section after a phase-space
integration, however will remain in differential distributions.
Obtained results are listed in Table-1 and Figs.9-10. Both of a total cross sections and differential distributions show a very good agreement with an exact calculations.